Newton-Raphson Method를 이용한 옵션 내재 변동성 산출

일반적으로 옵션의 이론적인 가격은 변동성 에 의해 결정되며 옵션의 (이론)가격=와 같이 표현된다.

하지만, 실제 시장에서 형성되는 옵션의 가격은 수요자와 공급자, 즉, 매수자와 매도자에 의해 가격이 형성되다보니 이론적으로 산출한 이론가격과 괴리를 나타낼 수밖에 없고 이에 따라 실제 형성된 옵션의 가격을 뒷받침해주는 변동성¹을 산출하려는 시도²)가 꾸준히 이어져왔다. 본 글에서는 제목에서 언급한 Newton-Rapshon Method를 이용하여 옵션, 그 중에서도 지수옵션³의 내재 변동성을 산출하는 일련의 흐름을 알아보고 개발 새발 작성된 본인의 관련 C source도 같이 알아본다.

먼저 시장에서 형성된 옵션의 가격은 [그림 1]과 같이 표현될 수 있다.

”]
 
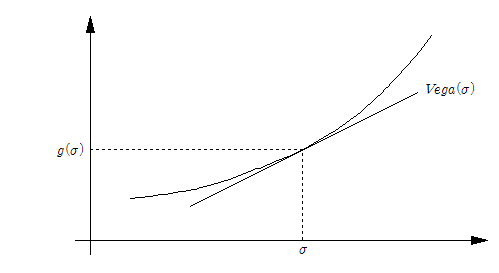
[그림 1]에서 보면, 형성된 가격은 와 같고 이 가격을 형성하는 변동성은 임을 알 수 있다. 또한 에서의 기울기는 옵션 민감도⁴ 중의 하나인 가 되는데, 이 가 곧 일 때의 옵션의 가격인 에서의 1차 도함수 값이 된다. 그런데, 문제는 옵션의 가격인 는 시장에서 확인이 되지만, 그 가격을 형성한 의 값은 모른다는 것이다. 그래서 이 를 찾기 위해 시행착오법(Trial & Error Method)을 통해 를 구해야 하기에 위 [그림 1]을 아래 [그림 2]처럼 약간 변경해준다.

”]
 
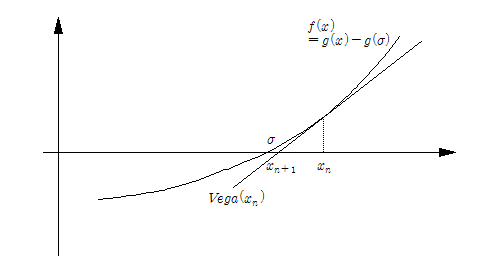
어차피 Newton-Raphson Method가 미분을 활용하여 ‘해’에 접근하는 방법이기 때문에 [그림 2]로부터 과 같은 식을 도출할 수 있게 된다. 이 식을 토대로 옵션의 가격 의 해인 에 근접하는 를 오차 범위 ⁵ 내에 도달할 때까지 반복해서 산출한다.

이 방법을 토대로 개발 새발 작성된 C source는 아래와 같다.

위 source에서 Options_TP, VegaO 등의 함수는 각각 이론가격 산출 및 민감도 Vega 산출 함수이다.

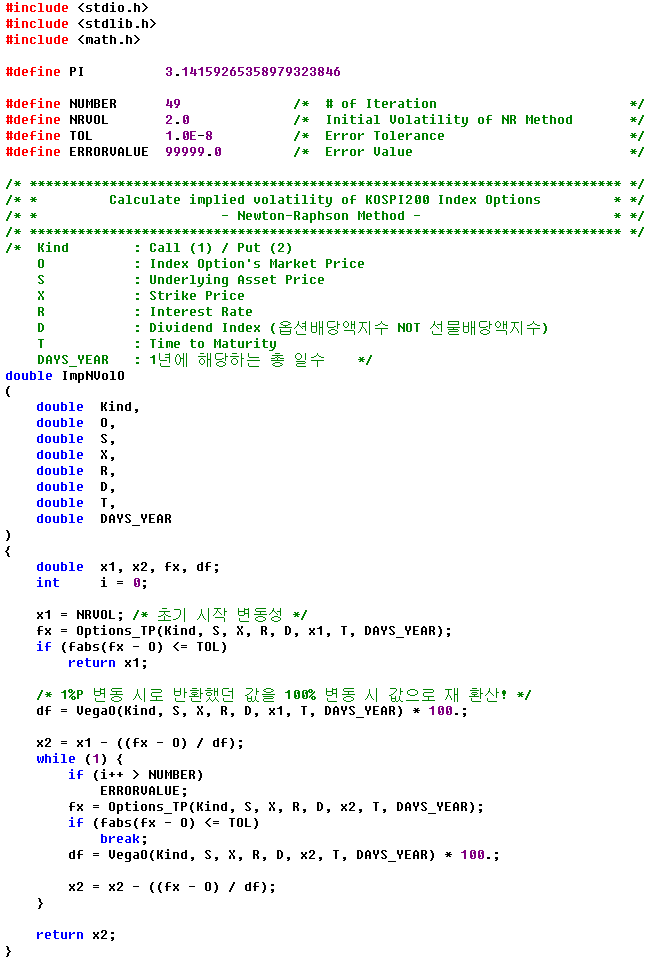
덧.: 시행착오법의 한계인 ‘해‘로의 ‘수렴‘이 아니라 ‘발산‘이 이루어질 경우, ‘근사해‘를 구할 수 없게 되기 때문에 iteration에 제한을 두고 있다.

1. 이를 옵션의 내재 변동성 또는 Implied Volatility라고 한다.
2. 수치해석학을 이용한 시행착오법(Trial & Error Method
3. 지수옵션, 주식옵션, 통화옵션 등의 유럽형 옵션이 현재 시장에 상장되어 있고 이론적으로 산출하는 각 옵션의 산출식은 대동소이하기 때문에 세부 논의는 생략한다.
4. Delta, Gamma, Vega, Theta, Rho
5. 보통